kaggle泰坦尼克号生存预测-随机森林

titanic
泰坦尼克号（RMS Titanic）的沉没是历史上最被人熟知的一次沉船事件。1912年4月15日，在她的处女航中，泰坦尼克号在与冰山相撞后沉没，在2224名乘客和机组人员中造成1502人死亡。这场耸人听闻的悲剧震惊了国际社会，并导致了更好的船舶安全规定。造成海难失事的原因之一是乘客和机组人员没有足够的救生艇。尽管幸存下沉有一些运气因素，但有些人比其他人更容易生存，比如女人，孩子和上流社会。
这个实验将进行乘客的存活分析，来预测哪些乘客幸免于难。

原始数据

kaggle的原始数据提供如下：

train.csv（训练集1:891）
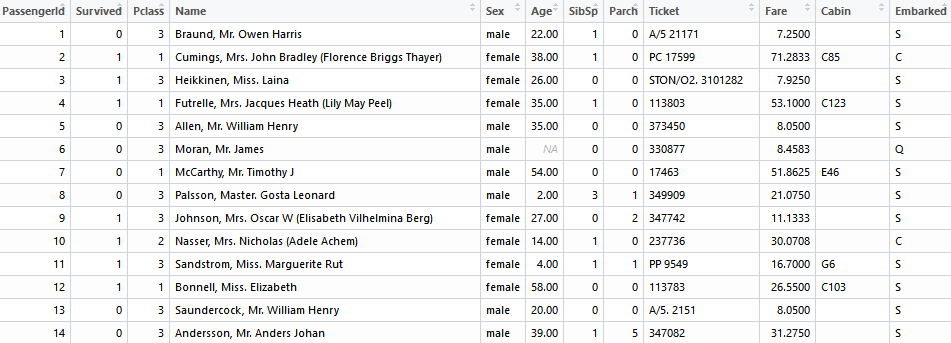
test.csv（测试集892:1309）
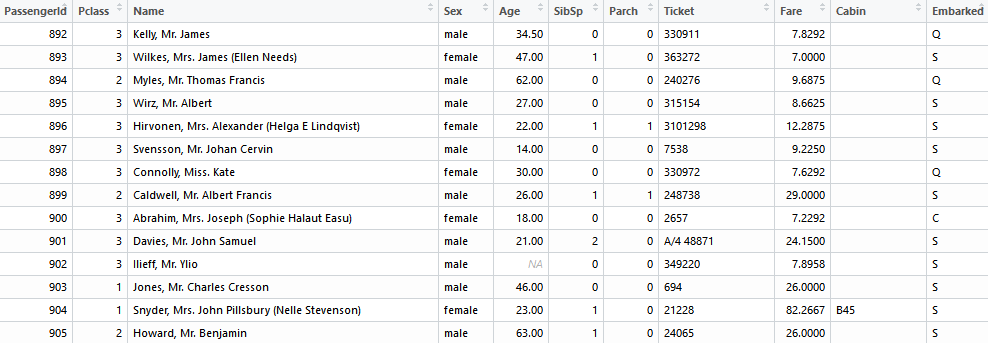
gender_submission.csv(真实结果)

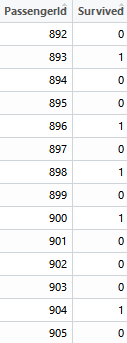
总共含1309条数据，每一行数据代表一个乘客的信息，因变量Survived表示是否幸存（1表示幸存，0表示没有）。除了因变量外，还考虑下面的解释变量，这些变量都能直接或间接地影响乘客能否幸存：

社会经济地位 (Pclass)：1=上，2=中，3=下；社会经济地位越高，受重视程度越高，直观上越容易得到救援；
姓名 (Name)：姓名决定了家族，一定程度上反映了乘客的社会地位；
性别 (Sex)：女士优先这个思想也决定了女性更容易得到关注，这里male表示男性，female表示女性；
年龄 (Age)：尊老爱幼也是一种美德，我们这里研究孩子和成人在事件(是否幸存)上的影响；
兄弟姐妹及配偶 (SibSp)、长辈和子女 (Parch)：该指标为计数指标，联合反映家庭人数的多少，单人出游计为0；
票码 (Ticket)：该指标反映了包括你在船上的位置信息等；
票价 (Fare)：票价决定了在船上的位置（有钱坐头等舱类似的情况）；
客舱号 (Cabin)：该指标类似票价可在一定程度上反映经济实力，其次遇难时船体的断裂点和该指标有直接联系；
登船港口 (Embarked)：该指标可以将乘客分类，使预测效果更好，这里C=瑟堡，Q=皇后镇，S=南安普敦.

数据处理加工

需要使用的包

library('ggplot2') #可视化
library('ggthemes') #可视化
library('scales') #可视化
library('dplyr') #数据加工
library('mice') #缺失值处理
library('randomForest') #随机森林

读取数据

train <- read.csv("train.csv")
test <- read.csv("test.csv")
fault<- read.csv("gender_submission.csv")
full<-bind_rows(train,test)

变量处理

看过泰坦尼克号电影的都知道，船长让女人和孩子优先上救生船，所以这里先对女性特征做一些简单处理：

构造新的分类变量：称呼（尊称）Title
从名字中可以提取前缀类似Miss,Dr…这些前缀可以反映该乘客的社会角色，从而将乘客更好的分类。

-------------------点击显/隐代码

full$Title <- gsub('(.*, )|(\\..*)','',full$Name)#正则替换
table(full$Sex,full$Title)

# 稀有前缀(数量少的合并)
rare_title <- c('Dona', 'Lady', 'the Countess','Capt', 'Col', 'Don', 
                'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer')
full$Title[full$Title == 'Mlle']        <- 'Miss' 
full$Title[full$Title == 'Ms']          <- 'Miss'
full$Title[full$Title == 'Mme']         <- 'Mrs' 
full$Title[full$Title %in% rare_title]  <- 'Rare Title'

table(full$Sex,full$Title)
# 从乘客姓名中取名
full$Surname <- sapply(full$Name,  
                      function(x) strsplit(x, split = '[,.]')[[1]][1])

下面是处理后的分类情况：
Title

构造新变量:家庭大小Fsize
在这里我们将兄弟姐妹及配偶，长辈和子女的个数综合起来构造新变量，代表家庭大小。
1
2
full$Fsize <- full$SibSp + full$Parch + 1
full$Family <- paste(full$Surname, full$Fsize, sep='_')

下图为家庭人数对生存情况的影响：

-------------------点击显/隐代码

# 查看家庭人数对生存情况的影响
ggplot(full[1:891,], aes(x = Fsize, fill = factor(Survived))) +
  geom_bar(stat='count', position='dodge') +
  scale_x_continuous(breaks=c(1:11)) +
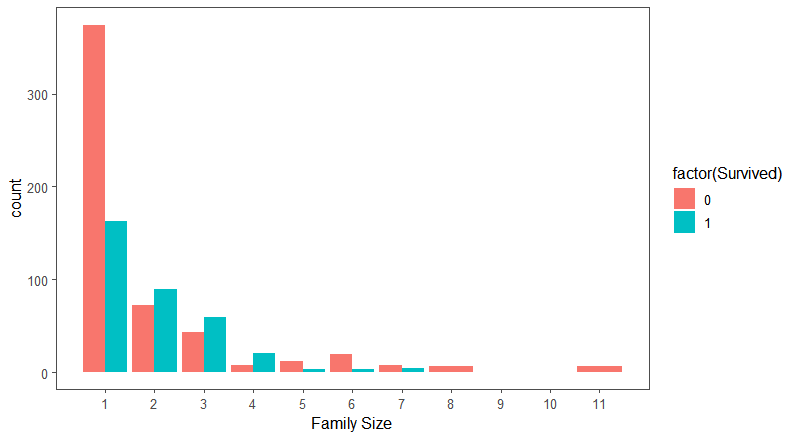
  labs(x = 'Family Size') +
  theme_few()

可以得到结论：

在总体上，女性幸存者多于男性；
随着家庭人数的增加，女性幸存者和男性幸存者的比例有先降后增的趋势。

重新定义成分类变量FsizeD：1个人为singleton,2-4个人为small,5人及以上为large，并做马赛克图。

-------------------点击显/隐代码

full$FsizeD[full$Fsize==1] <-'singleton'
full$FsizeD[full$Fsize<5 & full$Fsize>1] <-'small'
full$FsizeD[full$Fsize>4] <- 'large'

mosaicplot(table(full$FsizeD,full$Survived),main='Family Size by Survival',shade = TRUE)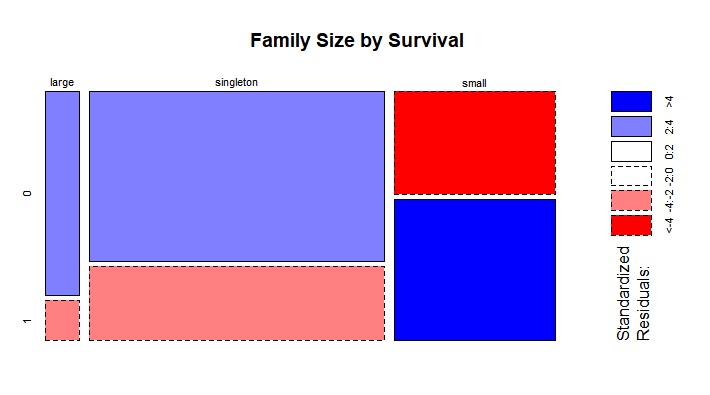

马赛克图表明：家庭规模对生存有惩罚效应.

由于Cabin变量的缺失数据太多，暂时不做处理，在后面也不纳入分析

缺失值处理

缺失值情况
1
md.pattern(full)

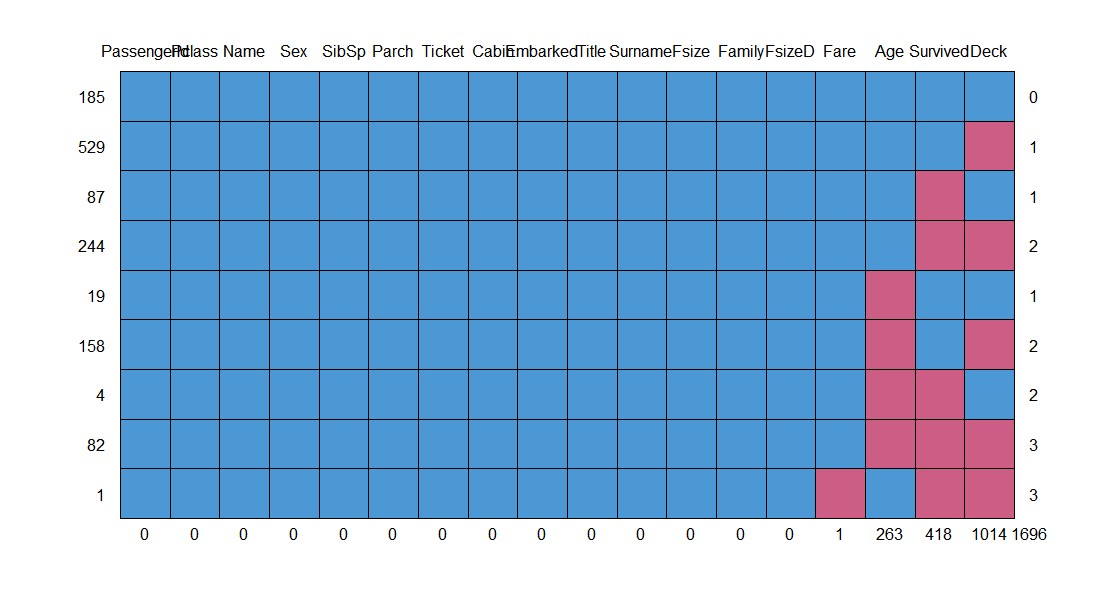
queshi1

Embarked缺失值处理

-------------------点击显/隐代码

full[c(62,830),c('Embarked','Fare')]

embark_fare <- full %>%
  filter(PassengerId != 62 & PassengerId != 830)
# 绘图
ggplot(embark_fare, aes(x = Embarked, y = Fare, fill = factor(Pclass))) +
  geom_boxplot() +
  geom_hline(aes(yintercept=80), 
    colour='red', linetype='dashed', lwd=1) +
  scale_y_continuous(labels=dollar_format()) +
  theme_few()
 
full$Embarked[c(62,830)] <- 'C' #填补缺失值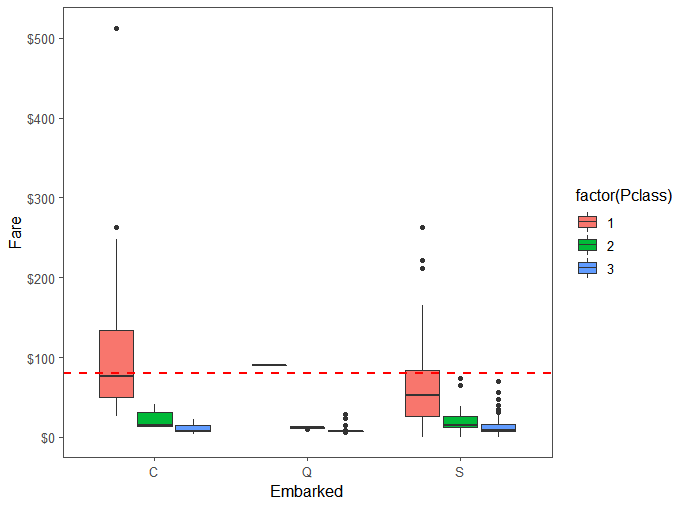

avarage
我们根据票价和登船港口确定来填补缺失值，Id为62和830的乘客缺少登船港口数据，其票价均为80$，观察票价和登船港口的情况发现：均值所在为80$的大概为C港，故将缺失值填补为C。

Fare缺失值处理
该变量包含一个缺失值，该缺失值情况如下：
Fare缺失数据
这是一个S港的三等 男性乘客，在这里用S港 三等乘客的票价中位数代替缺失值，票价替换为8.05$。

-------------------点击显/隐代码

ggplot(full[full$Pclass == '3' & full$Embarked == 'S' & full$PassengerId!=1044, ], 
  aes(x = Fare)) +
  geom_density(fill = '#99d6ff', alpha=0.4) + 
  geom_vline(aes(xintercept=median(Fare, na.rm=T)),
    colour='red', linetype='dashed', lwd=1) +
  scale_x_continuous(labels=dollar_format()) +
  theme_few()
# 中位数代替
full$Fare[1044] <- median(full[full$Pclass == '3' & full$Embarked == 'S',]$Fare,na.rm = TRUE)

mid

Age缺失值处理
1
sum(is.na(full$Age))

该变量包含263个缺失值，下面创建基于其他变量预测年龄的模型，并用mice进行多重插补法填补Age的缺失值。

-------------------点击显/隐代码

factor_vars <- c('PassengerId','Pclass','Sex','Embarked',
                 'Title','Surname','Family','FsizeD')
full[factor_vars] <- lapply(full[factor_vars], function(x) as.factor(x))
#随机种子数
set.seed((129))
# 排除某些不太有用的变量
mice_mod <- mice(full[, !names(full) %in% c('PassengerId','Name','Ticket','Cabin','Family','Surname','Survived')],
                 method='rf')  #rf为randomForest

# 保存完成输出
mice_output <- complete(mice_mod)
# 模型的结果替换原Age变量
full$Age <- mice_output$Age

将得到的结果与乘客年龄的原始分布进行比较，以确保没有任何完全错误：

par(mfrow=c(1,2)) #画布一分为二
hist(full$Age, freq=F, main='Age: Original Data', 
  col='darkgreen', ylim=c(0,0.04))
hist(mice_output$Age, freq=F, main='Age: MICE Output', 
  col='lightgreen', ylim=c(0,0.04))

age
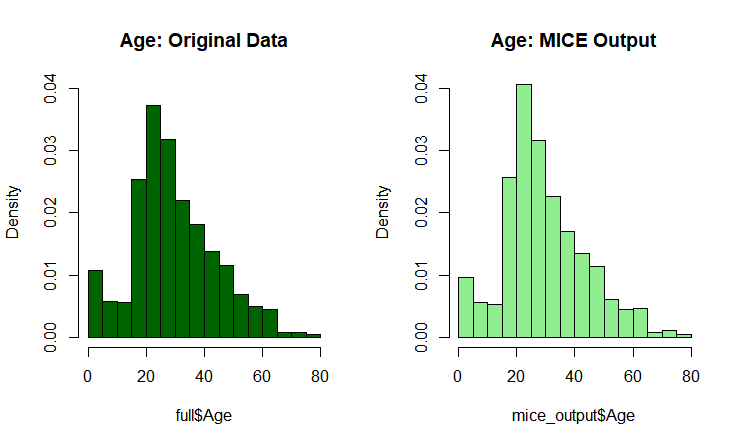
由图可知填补后的分布和之前的分布几乎一样，表明填补效果较好。

特征工程

先查看年龄和生存的关系（性别分组）：

ggplot(full[1:891,], aes(Age, fill = factor(Survived))) + 
  geom_histogram() + 
  facet_grid(.~Sex) + 
  theme_few()

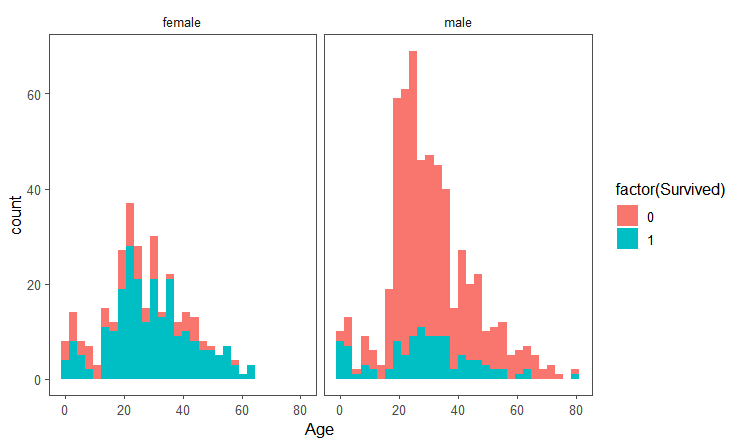
sheng_cun_guan_xi
由图：

男性的数量多于女性；
女性幸存者比率要远高于男性；
无论男性还是女性，18岁以下孩子的生存率是大致相同的；

这表明孩子和女士确实在灾难中得到了较多的帮助。

下面进行的特征工程的任务主要是创建新的分类因变量————孩子和母亲。
孩子标准如下：

大于0岁小于18岁

1
2
3

full$Child[full$Age < 18] <- 'Child'
full$Child[full$Age >= 18] <- 'Adult'
table(full$Child,full$Survived)

母亲标准如下：

女性
超过18岁
超过0个孩子

前缀没有’Miss’

1
2
3

full$Mother <- 'Not Mather'
full$Mother[full$Sex == 'female' & full$Parch > 0 & full$Age > 18 & full$Title != 'Miss'] <- 'Mother'
table(full$Mother,full$Survived)

最后将变量转为因子型完成建模前的数据处理。

full$Child <- factor(full$Child)
full$Mother <- factor(full$Mother)
par(mfrow=c(1,1))
md.pattern(full)

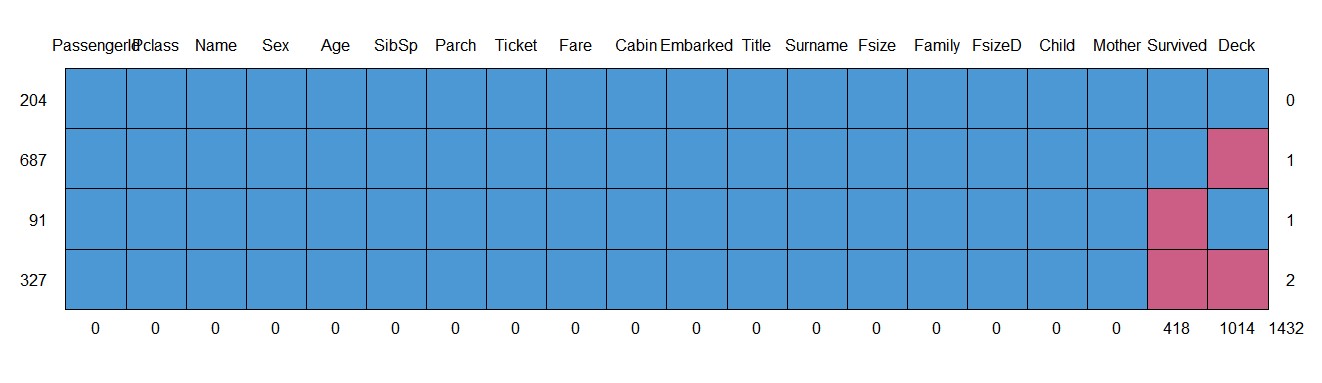
queshi2
此时除了需要预测的418个值和不纳入考虑的变量Deck以外没有其他缺失值。

随机森林模型(randomForest)

建模

划分训练集和测试集：

1 2	train <- full[1:891,] test <- full[892:1309,]

设定随机种子数
1
set.seed(300)

确定模型自变量

rf_model <- randomForest(factor(Survived) ~ Pclass + Sex + Age + SibSp + Parch + 
                                            Fare + Embarked + Title + 
                                            FsizeD + Child + Mother,
                                            data = train)
rf_model

选取除IDPassengerId,姓名Name,票码Ticket,客舱号Cabin,姓Surname以外的变量进行随机森林的建模，结果如下：
model
默认500棵随机树在训练集上表现出16.72%的估计错误率，意味着有八成的正确率；混淆矩阵表明幸存者被错误估计的比例为28.07%，未幸存者被错误估计的比例为9.65%。

变量重要性

下面我们查看变量对预测结果的重要程度：

-------------------点击显/隐代码

importance    <- importance(rf_model)
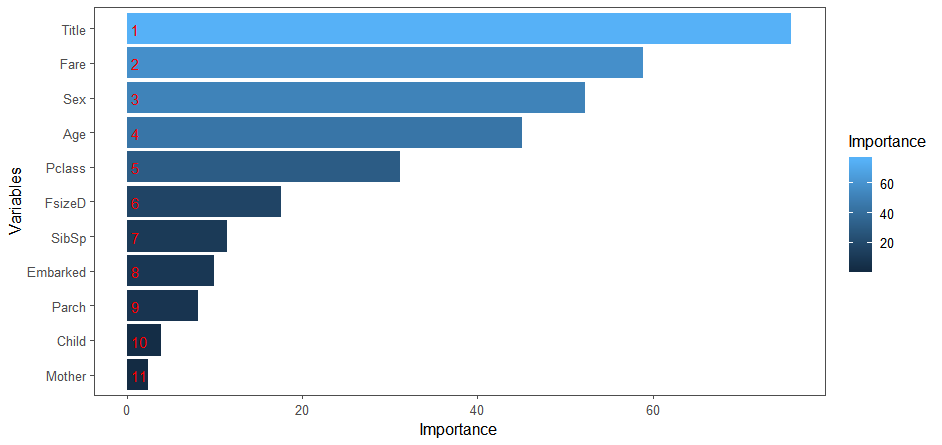
varImportance <- data.frame(Variables = row.names(importance), 
                            Importance = round(importance[ ,'MeanDecreaseGini'],2))
rankImportance <- varImportance %>%
  mutate(Rank = dense_rank(desc(Importance)))

ggplot(rankImportance, aes(x = reorder(Variables, Importance), 
    y = Importance, fill = Importance)) +
  #条形
  geom_bar(stat='identity') +
  #添加文字
  geom_text(aes(x = Variables, y = 0.5, label = Rank),
    hjust=0, vjust=0.55, size = 4, colour = 'red') +
  labs(x = 'Variables') +
  coord_flip() + 
  theme_few()

人为构造的变量Title在预测变量中具有最高的相对重要性，其后依次是票价、性别、年龄、社会经济地位……

人为构造的母亲分类从结果看并没有那么理想，可能是家人外出游玩，母亲需要留在家中的缘故。

预测

1
2
3

prediction <- predict(rf_model, test)
solution <- data.frame(PassengerID = test$PassengerId, Survived = prediction)
total <- data.frame(fault$PassengerId,fault$Survived,solution$Survived)

接着将预测结果和真实结果（保存在gender_submission.csv中）进行比较，得出正确率。

library(gmodels)
CrossTable(fault$Survived,solution$Survived,
           prop.chisq = FALSE,prop.c = FALSE,prop.r = FALSE,
           dnn = c('真实值','预测值'))

compare
得到的结论如下：

总体预测正确率为0.581+0.311=89.2%;
原本没幸存的乘客被预测成幸存的错误率为5.5%;
原本幸存的乘客被预测为没幸存的错误率为5.3%.